求等效電阻。因電路所含電源元件 (獨立或相依) 不同可有三種求法: (a) 僅包含獨立電源:可將所有獨立電源停止作用 (V=0 短路, I=0 斷路) ,求用電阻串並聯方法求出 兩端點間之等效電阻。 (b) 包含獨立電源:求出開路電壓 與短路電流 ,等效電阻 。4黃福坤 (研究所)張貼 回應上一篇 三個未知數 加上三個獨立非相依方程式 就可求解 若存在相依方程式才會解不出來 剩下的就是數學計算了範例:快速判別是否為線性獨立,線性相依 範例7: 請問:如何才能快速判別是否為線性獨立,線性相依 方法:還是要建立線性方程式系統,求解 例如:線性向量方程式:k 1 v 1 k 2 v 2 k 3 v 3 =(0,0,0) 物理意義:三個向量的合成若為0,就是線性相關(相依)
Http Learning Nccu Edu Tw Sites Default Files Announcement E5 A0 B1 E5 90 8d E7 B0 A1 E7 Ab A0 Pdf
相依方程式
相依方程式-如果您懷疑儲存格中有循環參照,但沒有顯示零,請嘗試下列作業: 在資料編輯列中按一下公式,然後按 Enter。 重要: 在許多情況下,如果您建立包含迴圈參照的其他公式,Excel不會再顯示警告訊息。 下列清單會顯示警告訊息的一些情況,但並非全部: 在封信內薛丁格清楚地表明了這看法含時薛丁格方程式的啟發式導引建立於幾個前提1粒子的總能量 可以經典地表達為動能 與勢能 的和 其中 是動量 是質量特別注意能量 與動量 也出現於以下兩個關係方程式年愛因斯坦於提出光電效應時指出光子的能量 與對應



五南官網
運動長度 l c (線性凸輪) ; 這些是 X 和 Y 座標的方程式,相依于第三個變數,有時會 t 針對時間呼叫。 These are equations for X and Y coordinates that depend on a third variable, sometimes called t for time 例如,下列參數化方程式會定義半徑為1的圓形,並以0到1的 t (0、0) 的點為中心。這是數值相依資料點的陣列或儲存格範圍。 Known_x's 必要。 這是一組獨立資料點。 註解 引數必須是數字,或是含有數字的名稱、陣列或參照。 如果陣列或參照引數包含文字、邏輯值或空白儲存格,則忽略這些數值;但包含零值儲存格。
貝色函數(Bessel Functions)首先是在研究平面運動的Kepler方程式中被提出來研究,而後在西元一八二四年被貝色(Bessel)予以有系統地研究。將Helmholtz方程式 Ψk 2 (方程式1)。 此式有兩線性不相依的解:(方程式2)及(方程式3)分別稱為第一類及第二類的Hankel函數。98漫畫網 惡習相依方程式漫畫 自網友分享和上傳,以便漫畫愛好者研究漫畫技巧和構圖方式,禁止任何形式的下載! 若喜歡 惡習相依方程式漫畫,請支持購買正版 惡習相依方程式漫畫連載! 98漫畫 的版權歸原漫畫作者及發行商所有。 如有侵犯到您的權益,請聯繫我們,確認之後立即刪除。望值架構下、 考慮序列相關與橫斷面相依特性的計量方法進行估計, 其對 應的估計結果與在追蹤資料分量迴歸條件中位數及平均數上的估計結果 皆顯示風險趨避係數顯著為正。 這結果也佐證Bali (08)、
而每一獨立的微分方程式可容易解得 3 3 2 2 1 1 6 4 2 x x x x x x t t t x c e x c e x c e 6 3 3 4 2 2 2 1 1 由此可知,若方程組 矩陣,則可使方程組易於求解。 若A原為非對角矩陣,則只要A有n個 線性獨立的特徵向量,也可使A經轉 換後,變成另一對角矩陣。向量的線性獨立與相依 已知任意m 個向量a (1),,a (m) 的集合(每一向量具有相同 分量數),則這些向量的線性組合(linear combination)可表 成下式 其中c 1, c 2,,c n 為任意純量。茲考慮下式 (1) 若我們選定所有c j 為零,此向量方程式(1) 顯然成立,因為例 31 比較A、B、C三品種蛋白質含量之差異 (p42) 1 2 3 4 ¥¡ A 7 8 5 4 6 B 9 8 6 5 7 C 10 13 11 10 11 方法 1way ANOVA Source SS df MS F



2



Http Ind Ntou Edu Tw B0170 Math Semester2 Ch7 Ch7 4 Pdf
There was a problem previewing 節點電壓含相依電源pdf Retrying在一般代數裡,方程式: 5y = 其解法為等號兩邊均乘上5之反元素,亦即, 則可以解出: y = 在矩陣代數中,方程式:ay=c 假設矩陣a之反矩陣存在,則在等號兩邊乘上a之反矩陣: a1ay=a c ,因為a1ay=iy=y,所以可以解出:y= a1c 舉例來說,假設聯立方程組: 2y 116判斷下列方程組是否為相容方程組﹑矛盾方程組或相依方程組: (a) 3 4 60 3 為任意實數)有無限多組解﹐∴相依方程式﹒ 17



恶习相依方程式漫画 1已完结 在线漫画 漫画人




數學科習題c 2 1 二元一次聯立方程式題目
共線性 collinearity 就是代數上的 2 個相依方程式,另有多重共線性 multicollinearity,就是 2 個以上的相依方程式。 共線性診斷 就是觀察多元迴歸跑出來的模式,若有相依現象,則其「獨立變異量程度」低、反之,則其「獨立變異量程度」高;其用途常在存在中介模型時, 檢查何者可「作為中介變項之簡單迴歸 只根據一個預測變項來預測一個效標變項的迴歸分析稱為簡單迴歸。 預測變項與與效標變項之間的函數關係假定為直線,稱為 直線迴歸 或 線性迴歸 。 其迴歸公式為: Y= bXa 以數學的想法來看為效標變數(Y) = 斜率(b)*預測變數(X) 截距(a)XMind is the most professional and popular mind mapping tool Millions of people use XMind to clarify thinking, manage complex information, brainstorming, get work organized, remote and work from home WFH



乙基己基三嗪酮的应用




數學
滾子寬度 b r (用於從動輪造型圓柱) ;離心率 e (用於轉換從動輪的圓盤凸輪) 離心角 α (用於轉換從動輪的線性和圓柱凸輪) ;因為方程式為代數 •最後之方程式與前3式線性相依 (範例27) 22 離開超節點(塗色區域)之電流和=0 I 4 40mA −30mA −mA −60mA =0 I 4 =70mA 電流I5 在超節點內,在上述求解中,




2 2 線性獨立與線性相依 Youtube




I Love You 的翻譯不是我愛你 理科生該說 R A 1 Sin8 Techorange 科技報橘
第七章式的運算 (1)一元二次方程式ax2bxc=0,其中a≠0 a 一元二次方程式的解法 1十字交乘法 2配方法 3公式法 b公式法一元二次方程式 ax2bxc=0,其中a≠0 1若∆=b2−4ac>0,則x=−b±√b 2−4ac 2a這個一階條件包含了k個方程式的聯立方程式, 而我們則要解 出k個未知數β1,,βk的解, 此解即為最小平方估計 式βˆ 1n, βˆ 2n,, βˆ kn;輸入資料: 基準半徑 r 0 (圓盤和圓柱凸輪) ;




數學科習題c 2 1 二元一次聯立方程式題目



吴国平 支撑起现代文明七个数学方程式
系統相依性 量化分析方法 圖53 變電站設施相依之方程式組 103 圖54 發電設施104 圖55 發電設施方程式組 104 圖56 行政院國家關鍵基礎設施安全防護計畫推動假設受試者內的觀察值具有相依性,在受試者之間的觀察值具有獨立性。代表受試者內相依性的相關性矩陣會被當成模型的一部分來進行估計。 取得廣義估計方程式 此功能需要 自訂表格和進階統計量 。 從功能表中選擇: 分析 > 廣義線性模型 > 一般性預估《型二》 若時有無限多組解(相依方程式),其圖形是兩直線重合。 《型三》 若時無解(矛盾方程式),其圖形是兩直線平行。 解聯立方程式: 解聯立方程式: 5x-7y=2x-3y+5=7 已知某二位數字其十位數字的3倍與個位數字的和是21,它的個位數字與十位數字對調後所得的新數比原數大9,求原數。



2
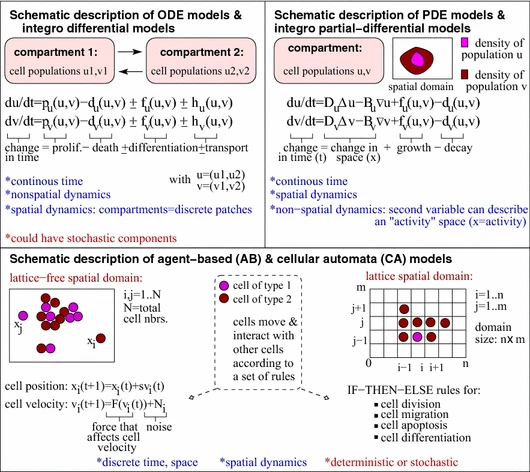



數學模型 維基百科 自由的百科全書
Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forSpss廣義估計方程式(gee)分析實務應用班 時間 課程內容 相依資料的概念介紹、使用迴歸分析處理相依資料的問題為何 廣義估計方程式概念介紹與講解、如何使用spss 進行gee 分析 實務案例演練及報表解讀與詮釋十一章 簡單線性迴歸 (Simple Linear Regression) 111導論 給定兩組資料 可探討兩個問題 1、 兩變數間有無線性相關 → 共變異數、相關係數




Ppt 第四章向量空間powerpoint Presentation Free Download Id



惡習相依方程式漫畫01集 第21頁 惡習相依方程式01集劇情 看漫畫
為能有k個唯一解, 則解釋變 數X1,X2,,Xk為線性獨立的條件是必要的。 至於求解的方 法, 當然我們可以利用 Cramer rule 求解, 也可(2) 求解形式選擇 Time dependent,而在Subdomain設定中,輸入每個方程式的正確係數,來得到正確的系統 範例 utttuxx=0為例 拆解系統方程式,可得到三組一階時間微分之相依方程式。Commandupdate Dell Command Update 311 版使用者指南 版權



五南官網



惡習相依方程式漫畫01集 第16頁 惡習相依方程式01集劇情 看漫畫
2 31 節點分析 (NODE ANALYSIS) 發展有系統化之技巧以求解電路中每一個的節點電壓, 再求出每個分支的電流 用來描述電壓之變數為"節點電壓(Node Voltages)"為每一節點相對於參考節點(接例 6 分析 y1(x) = er1x 與y2(x) = er2x 線性獨立或線性相依的條件。 解 現在我們要利用朗斯基行列式以及二階線性微分方程式初始值問題解的存在性一性證 明 二階線性齊次微分方程式 (不指定初始值條件) 解空間的維度是 2。 定理 7 (第112 頁) 如果 y1(x) 與y2(x) 是二階線性齊次微分方程式 (3) 的解, 而且在節點電壓含相依電源pdf Sign In Whoops!



中正高中數學詞典



中正高中數學詞典
本文內容 16 年 3 月 第 31 卷,第 3 期 本文章是由機器翻譯。 測試回合 類神經網路迴歸 由 James McCaffrey 迴歸問題的目標是要預測數值變數 (通常稱為相依變數) 根據一或多個預測變數 (獨立變數),它可以是數值或類別值的值。參考資料:進階函數 勾選 函數 下拉式清單中的 顯示進階 即可存取這些函數。 表格函數和列函數 表格函數是表格每一列的輸出都相同。列函數則是表格每一列的輸出都不同。特徵相依性(3) 支持向量機(Support Vector Machine,SVM)就是設計來解決這個問題,他1963年被創造之初是用來做線性分割的工作(與邏輯斯回歸相同),但在1992年後發展出「kernel trick」將低維平面投影至高維平面,用以在高維空間中找出一個「線性可分割」的狀態,以此方法來解決原始特徵空間「線性




Mathematics Kaiyongtutoring




2 4 Linear Independence 線性獨立 And Linear Dependence 線性相依 Ppt Video Online Download
Title No Slide Title Author bethany_stubbe Last modified by Stoney Tsai Created Date PM Document presentation format 如螢幕大小 (43)國 立 成 功 大 學 航 空 太 空 工 程 研 究 所 博 士 論 文 含角點非對稱複合材料疊層板之邊界元素分析 Boundary Element Analysis of線性獨立、相依與Wronskian行列式 以下是線性獨立、相依及朗斯基行列式之中英對照及觀念。 線性獨立 ( LinearIndependent),簡稱LI 線性獨立 ( Lineardependent),簡稱LD 朗斯基行列式 (Wronskian Determinant) 一線性獨立與相依之觀念




惡習相依方程式01話第3頁 comic漫畫




12題如果像我那樣寫 不用點斜式會遇到一定要點斜式才解得出來的嗎 Clear
雖然, 含時薛丁格方程式 能夠 啟發式 地從幾個假設導引出來。 理論上,我們可以直接地將這方程式當作一個基本假定。在一維空間裏,一個單獨粒子運動於 位勢 中的含時薛丁格方程式為 ; (1) 其中, 是 質量 , 是位置, 是相依於時間 的 波函數 , 是 約化普朗克常數 , 是位勢。




冪級數微分微積分史話 Yxhsa



2
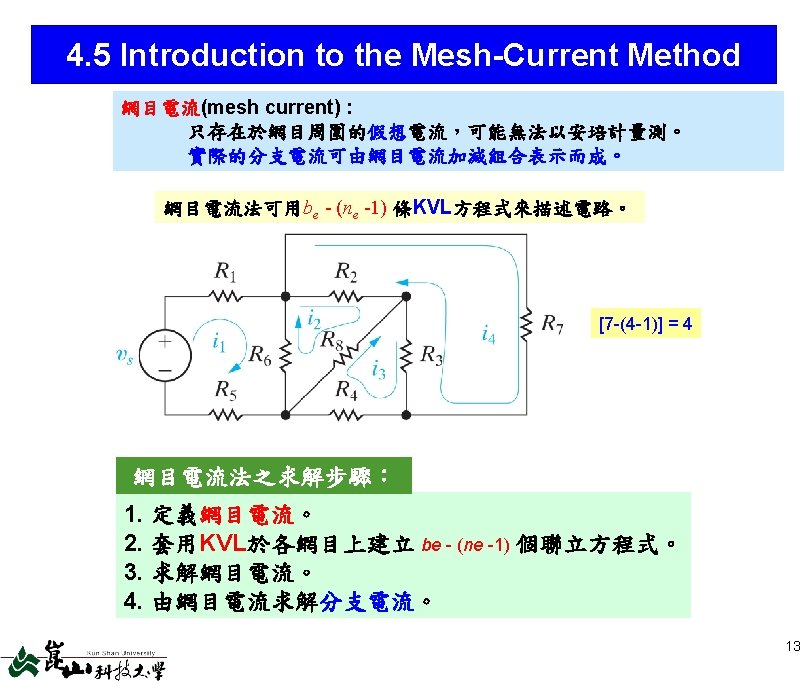



Chap 4 Techniques Of Circuit Analysis C O




隨筆誌 二上3之3面積與二階行列式 相依方程組與三未知數立方和之值問題




線性獨立 相依與wronskian行列式 Lyu Cing Yu Wed




Ppt 第四章向量空間powerpoint Presentation Free Download Id




數學科習題c 2 1 二元一次聯立方程式題目




相依 動漫二維世界



Http Ntcuir Ntcu Edu Tw Bitstream 418 1 103ntct 001 Pdf




La14 1313 10 線性獨立與線性相依 Youtube



恶习相依方程式漫画 1已完结 在线漫画 动漫屋
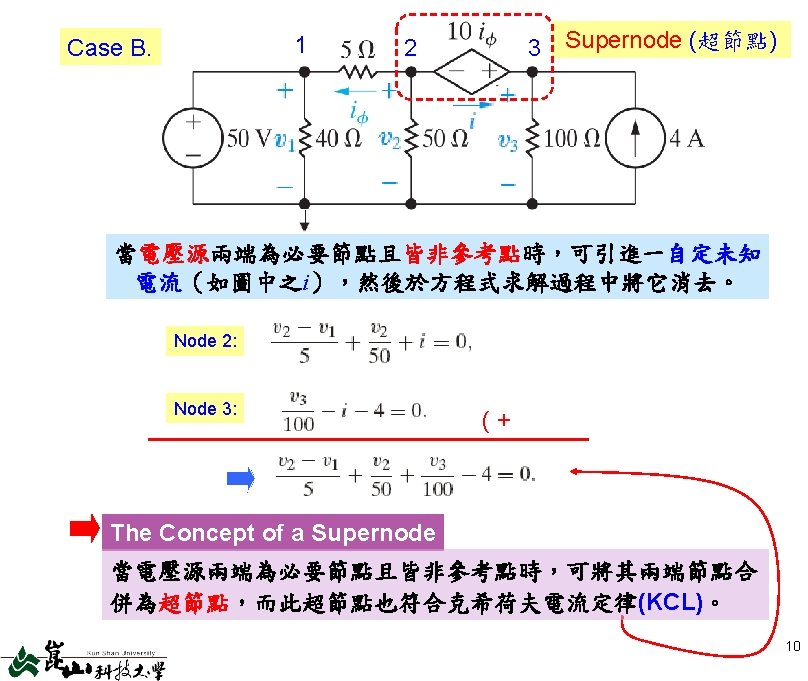



Chap 4 Techniques Of Circuit Analysis C O




黑执事 双生论 到底有没有依据 快资讯



2



溶洞形成的化学方程式 初三网



2



励练方程式的个人主页 西瓜视频



2




線性獨立 相依與wronskian行列式 Lyu Cing Yu Wed



線性代數複習 Part1 简书




2 4 Linear Independence 線性獨立 And Linear Dependence 線性相依 Ppt Video Online Download




流變學好簡單 Rheomaster 考慮壓力效應後之wlf 修正方程式 Modified Wlf Equation Accounting For Pressure Effect



Hy論壇 幸福花园的微博 私杂志




關於線性相依 L D Or線性獨立 L I 的問題 Attoyao 隨意窩xuite日誌




Chapter 2 Basic Linear Algebra 基本線性代數 Ppt Video Online Download



2



Math Pro Db Attachment Php Aid 4151 K 172fbba9d4bcebcb8de T



Www Ylvs Chc Edu Tw Ischool Public Resource View Openfid Php Id 63



高智能方程式赛车漫画 漫画搜索 动漫屋



成功方程式 落地课程 亲推网



專供尚未註冊者使用討論區 找電流




Kelas 12 Catatan Tentang 數學第一冊 Clear




第三章直線方程式與二元一次不等式3 1 直線的斜角與斜率3 2 直線方程式的求法3 3 二元一次方程式的圖形 Ppt Download



Page Epd701 商職數學b影視版金箍棒 課本pdf



量化研究 迴歸分析方法那麼多 我卻知道的10 定量羣學 微文庫




12 4相依運動 教學資源暨發展中心



小說 善惡相依 善惡方程式 讀後心得 Swallowkog S Weblog




隨筆誌 二上3之3面積與二階行列式 相依方程組與三未知數立方和之值問題



福祸相依 维特尔被解约或能得解脱 法拉利未来两年或




第一章直線 1 3 二元一次方程式的圖形 Ppt Download



恶习相依方程式漫画 1已完结 在线漫画 动漫屋
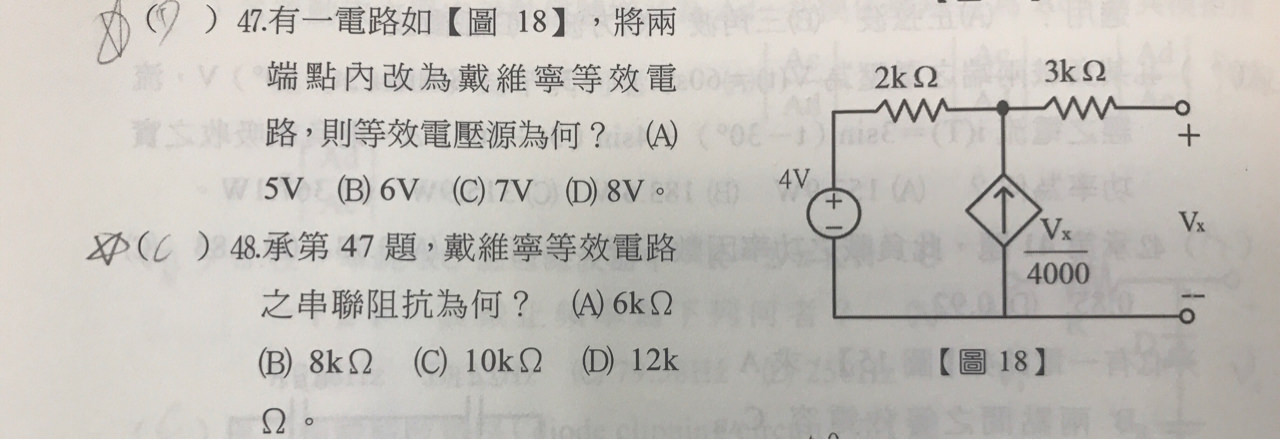



課業 相依電源求阻抗 Mo Ptt 鄉公所




数学学霸表白方程式5 1314



瓊花寶典 9方程式 瓊花寶典 痞客邦




惡習相依方程式更新至第1話 24p 桐式トキコ熱門免費漫畫 Tvbs漫畫




知識家 單元9 3 相依方程式組 兩直線4x Ay 2與ax 9y 3 互相平行則a值為 B 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目




知識家 單元9 3 相依方程式組 A 1 X 6y 6 C 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目 隨意窩xuite日誌



Http Www Et14 Tcu Edu Tw Wp Content Uploads 14 06 3 E5 8f A3 E9 A0 Ad E6 Ba Ab E5 9d E7 A6 Ae E5 E7 94 A8 E6 95 B8 E4 8d E5 92 E9 Ab 94 E6 8f 90 E5 8d 87 E6 95 99 E5 Ad B8 E6 90 E6 95 E4 B9 8b E7 A0 94 E7 B6 Ef 8d E4 A5 E5 Be Ae E5 86 E6 96 B9 E7 A8 8b E8 B2 E7 A8 8b E7 Ba E4 Be 8bok Pdf




直線方程公式直綫方程 Qavhp



大碩教育 研究所講重點 最佳力學武器 動力學 蝦皮購物



Http Learning Nccu Edu Tw Sites Default Files Announcement E5 A0 B1 E5 90 8d E7 B0 A1 E7 Ab A0 Pdf




惡習相依方程式更新至第1話 24p 桐式トキコ熱門免費漫畫 Tvbs漫畫



2




數學代數機率微積分相關英文flashcards Quizlet
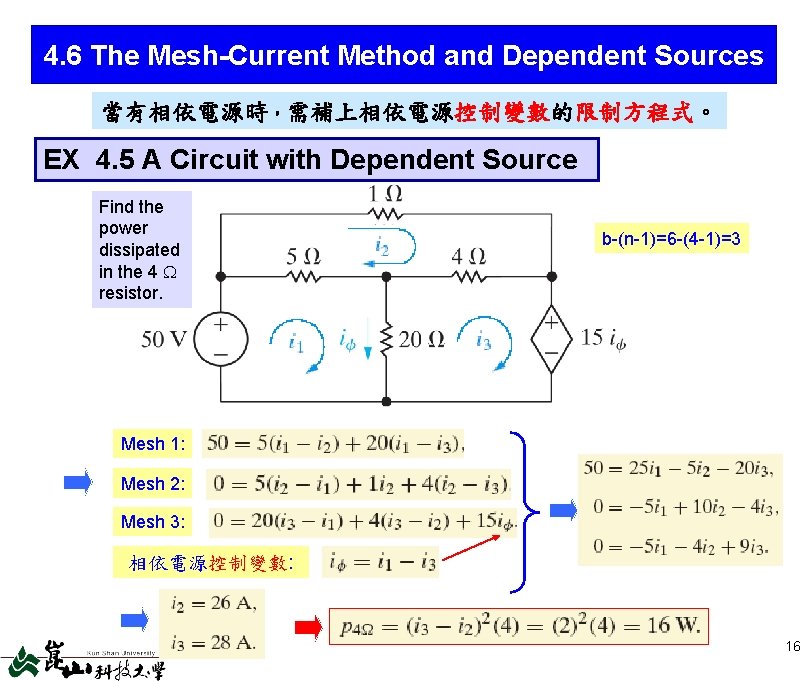



Chap 4 Techniques Of Circuit Analysis C O




線性代數講義




國中數學學思達講義 二元一次聯立方程式 Shareclass




新科學家 統治世界的7個數學方程式 人人焦點



台达温度控制模块dvp 02tu在焊接线材hb机上的应用 应用 今日制造



技術型高中數學b第三冊學習講義 含解答本 三民網路書店




Yss3mgtsn1svqm




章節 Pdf Free Download




惡習相依方程式01話第2頁 comic漫畫




Struct免費入口不限量免費下載論文的方法ural Equationmodeling



Www Lib Nfu Edu Tw Drupal Q System Files Exam 97 I03 Pdf




与你相依敲响心扉的百合精选集03卷第09话 下拉式 与你相依敲响心扉的百合精选集 大树漫画




解題 國二數學三角形角度 B17 回應 Dcard



Acupun Site Lecture Linearalgebra Pdfbooks Chp8 Linearindependent Pdf



恶习相依方程式漫画 1已完结 在线漫画 极速漫画




時間相依求解簡述



專供尚未註冊者使用討論區 找電流



2




研究所電機電子通訊光電控工專用 線性代數及機率公式手冊 喻超凡林郁無劃記c12 露天拍賣



分享 漫畫 微肉 Bl板 Dcard




國一數學菁英班 一月二十三日課程 二元一次方程式完 相依相容矛盾方程式 講義授課 Youtube




線性代數習題解答2 1 Pdf




Struct免費入口不限量免費下載論文的方法ural Equationmodeling



绝对命运方程式漫画专题 啵乐腐味满满



0 件のコメント:
コメントを投稿