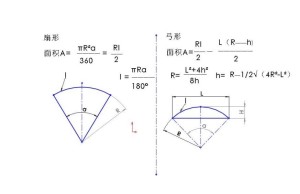
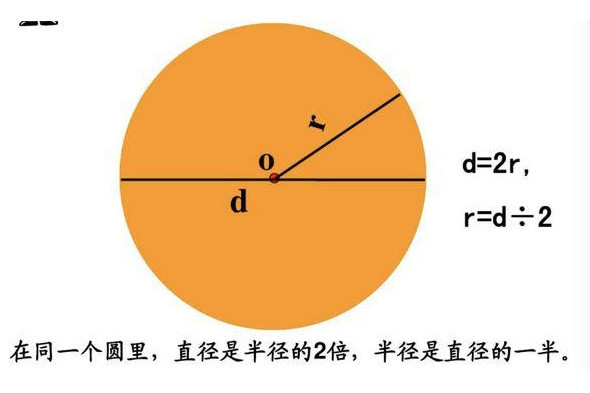
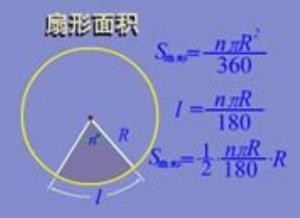
扇形の公式(計算式) 面積S,半径r,中心角x度,弧の長さl 面積S S = πr2 × x 360 S = π r 2 × x 360 弧の長さl l = 2πr × x 360 l = 2 π r × x 360 ホーム かんたん計算機 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。 式を変形 小文字になってしまっていますが気にし 覚え方 扇形の面積には、エッチなパイがあーる。 ┓ あなたがさりげなく書いておられた「半径は分かってる」とは 母線としての半径hと、底面の円の半径rとが分かってるということ

圓的周長與面積 扇形的面積計算練習 Youtube
扇形面積 計算
扇形面積 計算-円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 楕円の面積 楕円扇形の面積 楕円弓形の面積 放物線扇形の面積と円の面積、扇形の角度と円の角度の比率は同じなので、 S:πr 2 =θ:2π S2π=πθr 2 S=r 2 θ/2 です。扇形の面積が角度の大きさに比例することを利用して導いています。扇形の弧の
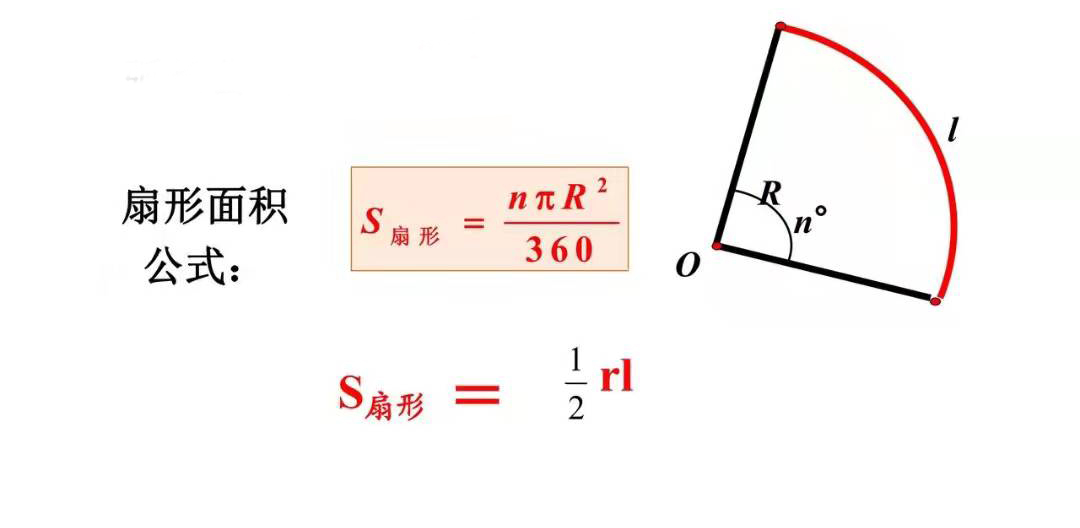



扇形面积公式 扇形面积公式推导 胡巴网
扇形の面積の求め方の公式! 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360 になるんだ。 つ扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明 エンジニアの学習・コミュニティーサイ
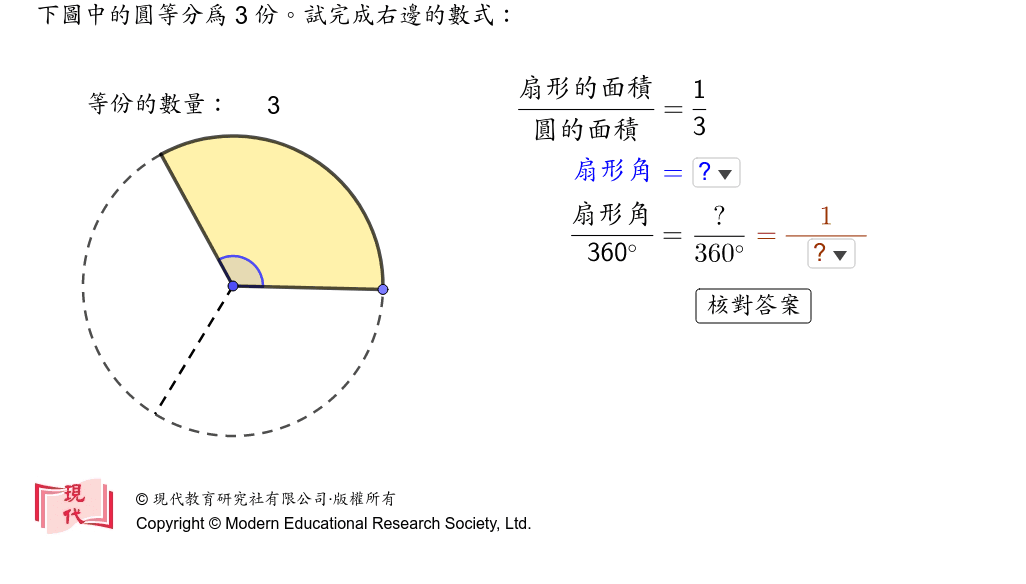
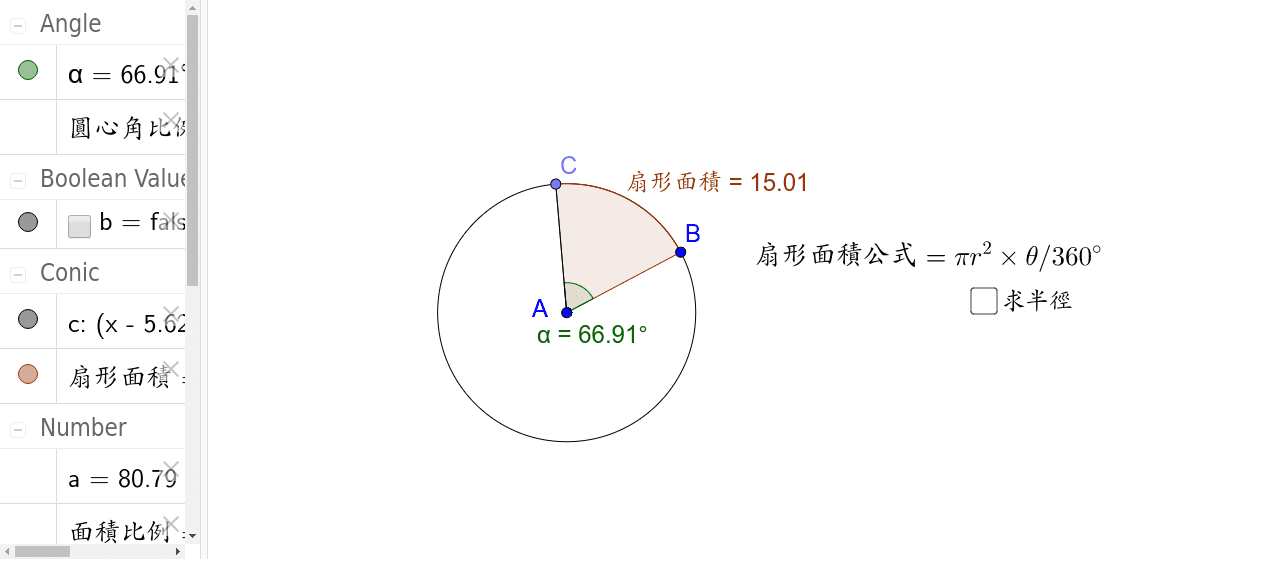
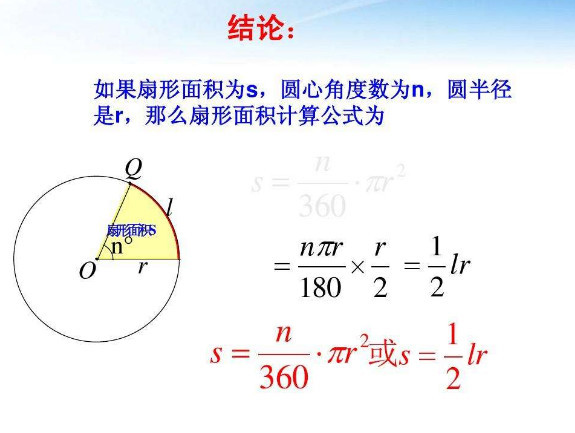
次の図のように,1辺の長さがa(cm)の正方形ABCDを頂点Bを中心として45°回転したとき,辺BA,ADが通過する部分の面積(cm 2) ヒント 黄色で示した直角二等辺三角形は回転して重なる.扇形の 面積 は、扇形の中心角を θ とした場合、 円の面積 × で求めることができます。 つまり、半径が r の扇形であれば、 面積 は、 r 2 π × で求まります。 なお、 θ = 3 6 0 ° のとき、 円の面積 に 扇形の面積を求めるときには次の公式を使います。 扇形の面積 =半径×半径×円周率× 中 心 角 360 ° ※扇形の面積は、円の面積に 中 心 角 360 ° をかけることで求めることが出来ます。
2分でわかる! 扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね? ? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、为圆周率*半径的平方,用字母可以表示为:S=πr²或S=π·(d/2)²。 (π表示圆周率(3 扇形面积公式 扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。 数学公式表示为:S まずは、方程式を使って扇形を求める方法について解説していきます。 求めたい中心角を とおいて、方程式を作っていきます。 中心角を とすると、問題文から弧の長さが与えられて




弧长和扇形面积 圆ppt 第1课时 下载 牛二ppt



專題訓練丨弧長和扇形面積同步練習 附答案 建議收藏 雪花新闻
扇形の面積、再考 2 角で挟まれる楕円の扇形 ここまで考えてきた楕円の扇形は x 軸とある中心角 で構成されるものであった。ここでは任意の と () で挟まれる扇形を考えたい。この面積 扇形面積公式描述了扇形面積和圓心角(頂角)、半徑、所對弧長的關係。 數學公式表示為:S扇=(lR)/2 (l為扇形弧長) = (1/2)θR² (θ為以弧度表示的圓心角)。 中文名 扇形面積公式 學 名前の通り, 弧度法 は円の「弧」をもとに定義されます. 半径 1 の扇形の弧の長さが θ であるとき,この扇形の中心角の大きさを θ rad と定める.ただし, rad は「 ラジアン
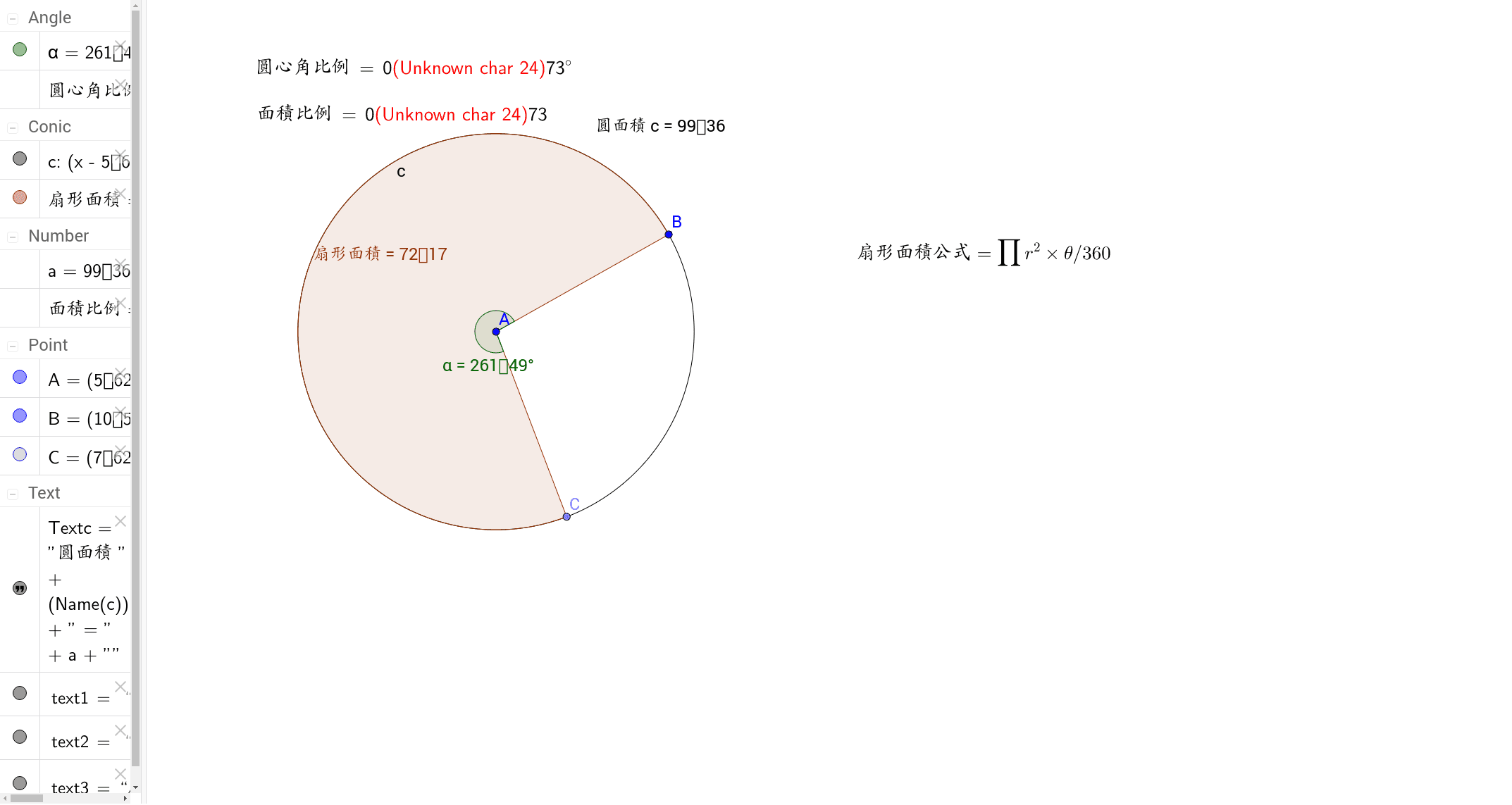



扇形面積公式 Geogebra




扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube
扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見談到扇形面積的計算,披薩就是生活中的一個案例,所有的披薩切開後都像扇形一樣。 舉例而言,若一塊披薩切割成六等分,每一片形狀皆為扇形,而披薩的半徑為 7 英寸,讓我們試著使用扇形面積公 扇形の面積 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成




扇形周长计算公式 圆与扇形的周长与面积计算 好房365
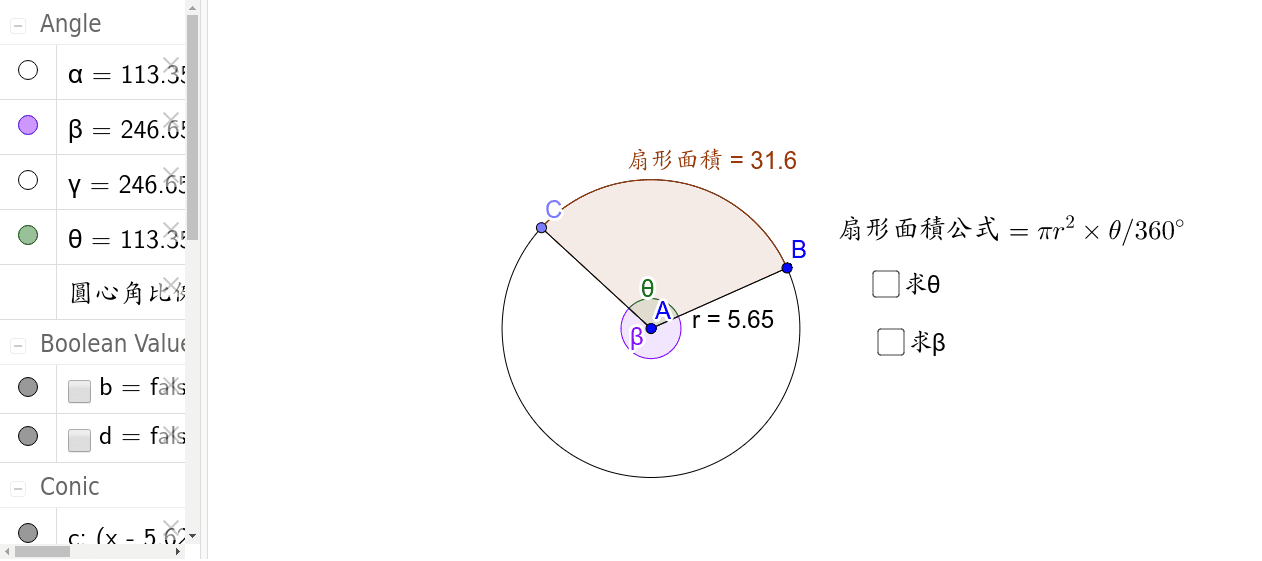



扇形面積公式3 Geogebra
扇形面積 公式: S扇=(lR)/2 (l為扇形弧長) = (1/2)θR² (θ為以弧度表示的圓心角) S扇=(n/360)πR² s扇=1/2lr(當知道弧長時) (n為圓心角的度數,R為扇形的半徑) 注:π為 圓周扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度極方程式で表される曲線の面積は,通常通り y y を x x で積分するよりもかなり速く求めることができます. 扇形に分割して積分 する方法です.ただし出現頻度はそこまで高くなく, バームクーヘン



数学长征 扇形面积 圆周率 Pi 派 圆周率的定义 圆周率小知识



扇形面积公式的注意点及应用 25 9弧长与扇形面积 初中沪科版13版 数学中国网 Mathschina Com
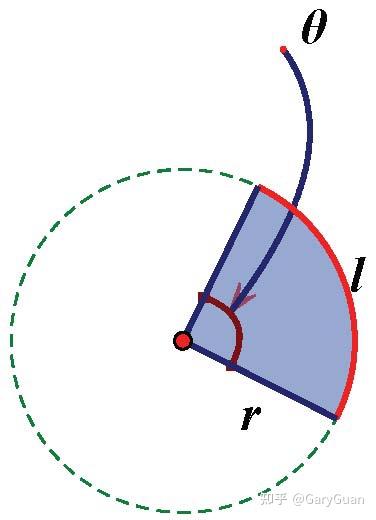
扇形是與圓形有關的一種重要圖形,其面積與圓心角(頂角)、圓半徑相關,圓心角為n°,半徑為r的扇形面積為πr 2 /360º×nº。 如果其頂角採用弧度單位,則可簡化為半徑乘弧長乘1/2 弧長 =半徑×弧度)よって,楕円の面積公式より答えは \pi \cdot 3\cdot 4=12\pi π ⋅ 3⋅ 4 = 12π ここから,楕円の面積公式の3通りの証明を紹介します。 グラフの拡大を用いる方法 愚直に定積分を計算する方法 ガウ扇形(おうぎがた、英 circular sector )は、平面図形の一つで、円の2本の半径とその間にある円弧によって囲まれた図形である。 数学的な記述 中心角 2本の半径がなす角を扇形の中心角という
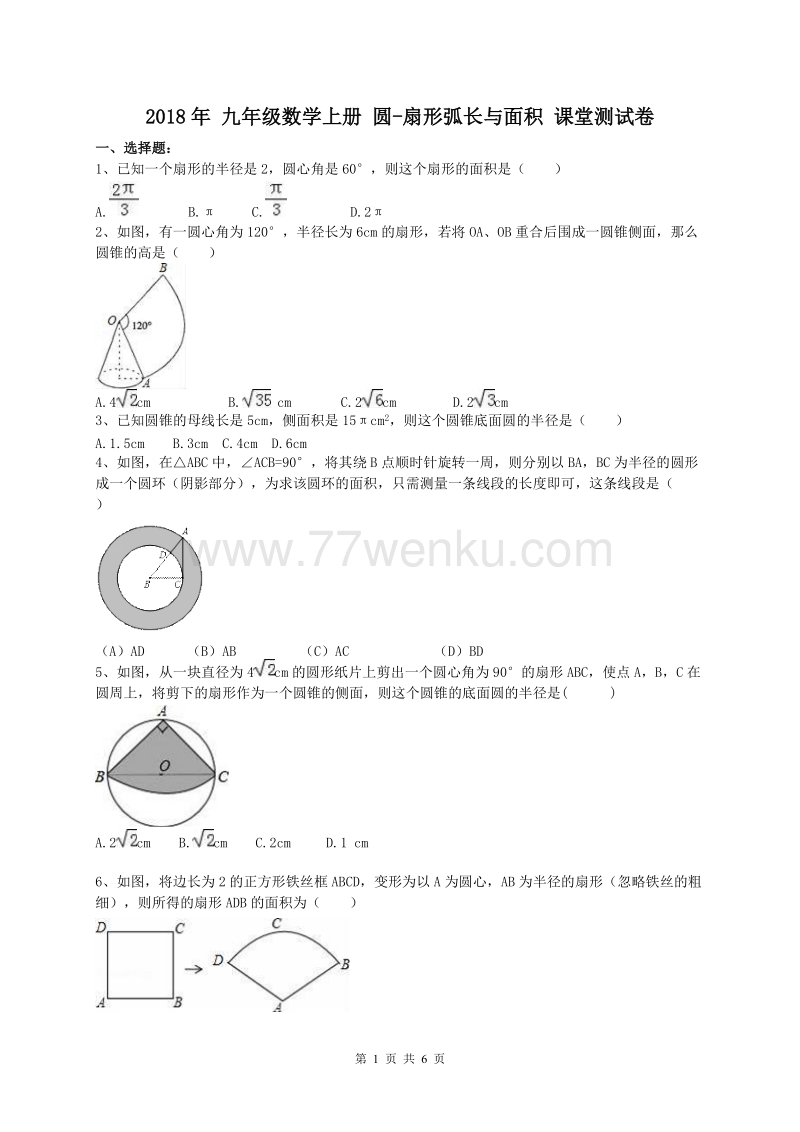



18年秋人教版九年级数学上册 24 4弧长和扇形面积 课堂测试卷含答案 七七文库www 77wenku Com



扇形面积 快懂百科
扇形の面積 S=r^2θ/2=rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は?1分でわかる意味、公式、求め方、 本頁面最後修訂於22年5月3日 (星期二) 1253。 本站的全部文字在創用CC 姓名標示相同方式分享 30協議 之條款下提供,附加條款亦可能應用。 (請參閱使用條款) Wikipedia®和維 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に大きな円はイメージできていますか? 弧の




圓的周長與面積 扇形的面積計算練習 Youtube



扇形面積公式 Geogebra
なぜわざわざ弧度法を使うのか、 弧度法のメリットを紹介します。 ・弧度法のメリット1つ目は、 弧の長さ,面積が簡単に求められます。 次の章「扇形の弧の長さと面積の公式」で解説するから分用 半徑、弧度 計算扇形面積 扇形面積 圓面積 弧度比例 圓周率 半徑 圓周率 半徑 扇 形 面 積 = 圓 面 積 × 弧 度 比 例 = 圓 周 率 × 半 徑 2 × θ r a d 2 × 圓 周 率 = 半 徑 2 2 × θ r a d = R 2 2 × θ r a d扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为nºπr²/360º。 如果其顶角采用弧度单位,则可简化为半径乘弧长乘1/2, 弧长 =半径×弧度)



面积公式 数学公式 搜狗百科



六年级扇形面积和弧长公式 初三网




课程学习 人教九上 24 4 弧长和扇形面积 1 弧长和扇形面积



初中数学 扇形的面积 教材 优课网



积分求平面图形的面积 玄数



扇形面积 数学术语 搜狗百科



扇形面积 讲思路讲方法 更讲简算习惯 这是很多老师也不会注意的一个细节 哔哩哔哩 Bilibili




扇形面积公式 百度百科




扇形面积怎么算 求扇形面积最有效的2种方法解析 易考号



表征模式5 与弧长 扇形面积有关的问题 基 简书




扇形面积 数学术语 搜狗百科




扇形面积公式



扇形面积公式 快懂百科



扇形周長題目




弧长和扇形面积 圆ppt下载下载 牛二ppt




扇形的面积公式 弧长公式 环球信息网



1




扇形面积公式和扇形弧长公式扇形的所有公式



扇形面积公式讲解 北京爱智康




扇形弧长 百度百科



初中数学 求阴影部分面积 如何计算不规则扇形面积呢 哔哩哔哩 Bilibili




第二十一讲弧长及扇形面积 暑假辅导班 21年新九年级数学暑假精品课程 浙教版 Zip 师客文库




扇形面积公式 扇形面积公式推导 胡巴网




请帮忙解答一道六年级的扇形面积题 篱笆社区手机版




19扇形面積數學習作訂正 林語婕 楊老師的部落格 痞客邦



Pjjgyrwzrk3rbm




专训24 4 1 弧长和扇形面积计算 简单数学之21 22学年九年级上册考点专训 人教版 Zip 师客文库




弧度制扇形面积公式 爱问教育培训




扇形面积公式小学 小风教程网



扇形面積公式2 Geogebra



80 定积分 曲边扇形的面积 哔哩哔哩 Bilibili



專題訓練丨弧長和扇形面積同步練習 附答案 建議收藏 雪花新闻



扇形面积 数学术语 搜狗百科




扇形面积怎么算 超实用的高中数学公式 碳资讯



扇形面积公式小学 初三网



扇形的面积公式 哔哩哔哩 Bilibili




圓及扇形面積 Geogebra




数学弧长公式扇形面积公式 九年级数学 弧长及扇形的面积 知识点回顾 碳资讯



六年级扇形面积公式 初三网




圓的周長與面積 19 扇形的面積計算 Youtube



扇形计算公式 数学公式 搜狗百科




三年中考真题 九年级数学上册24 4弧长和扇形面积同步练习 含答案 七七文库www 77wenku Com




数学九年级下册2 6 弧长与扇形面积同步测试题 教习网 试卷下载




关于弧长公式扇形面积公式的信息 猪扒资讯




扇形面積公式 百度百科




扇形周長固定求面積最大值 Youtube



國小數學六年級圓周長 圓面積和扇形面積 3 扇形周長與扇形面積吳政達濱江國小 Youtube




例題 扇形的面積計算 數學 均一教育平台



九年级数学 弧长及扇形的面积 知识点总结 扇形面积怎么求 拾味生活



扇形计算公式 数学公式 搜狗百科




弧长和扇形面积 圆ppt 第1课时 下载 牛二ppt



扇形面积公式 知乎




扇形的弧長與面積



数学长征 扇形面积 圆周率 Pi 派 圆周率的定义 圆周率小知识



3 9 弧长及扇形的面积 哔哩哔哩 Bilibili
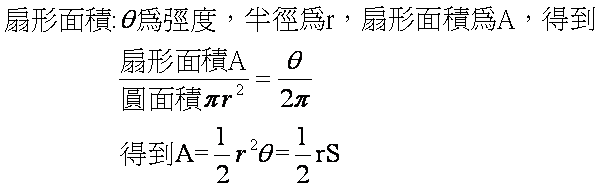



扇形的弧長與面積



圆的弧长公式和扇形面积公式圆的弧长公式和扇形面积公式初中 天奇生活




扇形面积公式是什么




初中数学 弧长及扇形面积问题的总结及练习 公式 有理数 世界



扇形周長公式



3 6 弧长和扇形面积的计算 Page104 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网



扇形进阶 容斥原理有关的面积题 哔哩哔哩 Bilibili
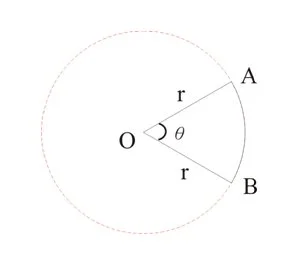



14 平面及立體圖形 扇形的面積及弧長 齊齊溫



22年 2 6 弧长与扇形面积 练习题 2 6 弧长与扇形面积 测试卷下载 湘教版数学九年级下册 教习网




圆扇形与弓形




3 8 弧长及扇形的面积同步测试 浙教版 Zip 师客文库




圓的周長與面積 27 扇形的複合圖行計算2 Youtube




六年级扇形面积公式
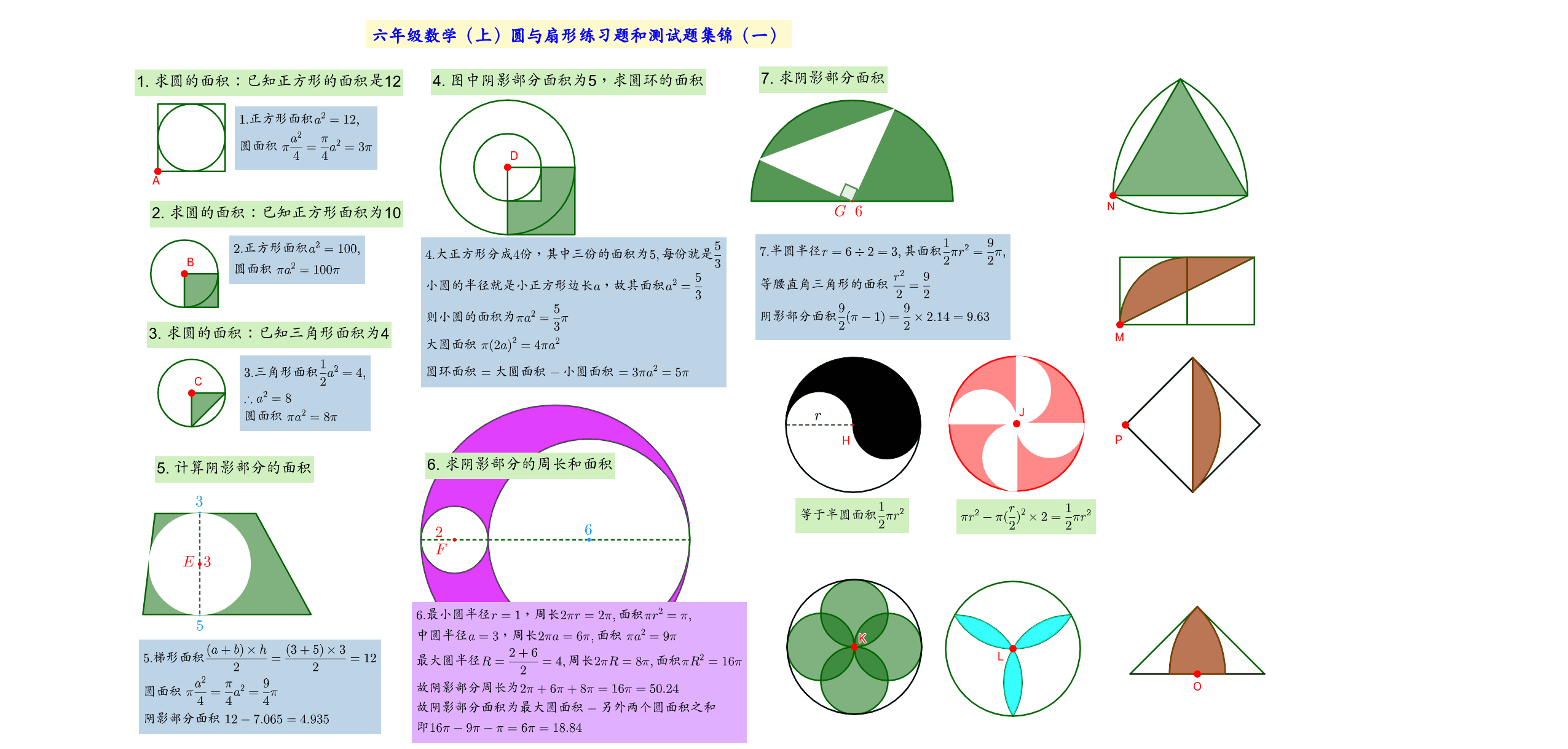



圆与扇形面积举例 Geogebra



题型 2弧长与扇形面积公式的计算 哔哩哔哩 Bilibili




弧长与扇形面积 沪科版初中数学初三数学下册电子课本 易学啦
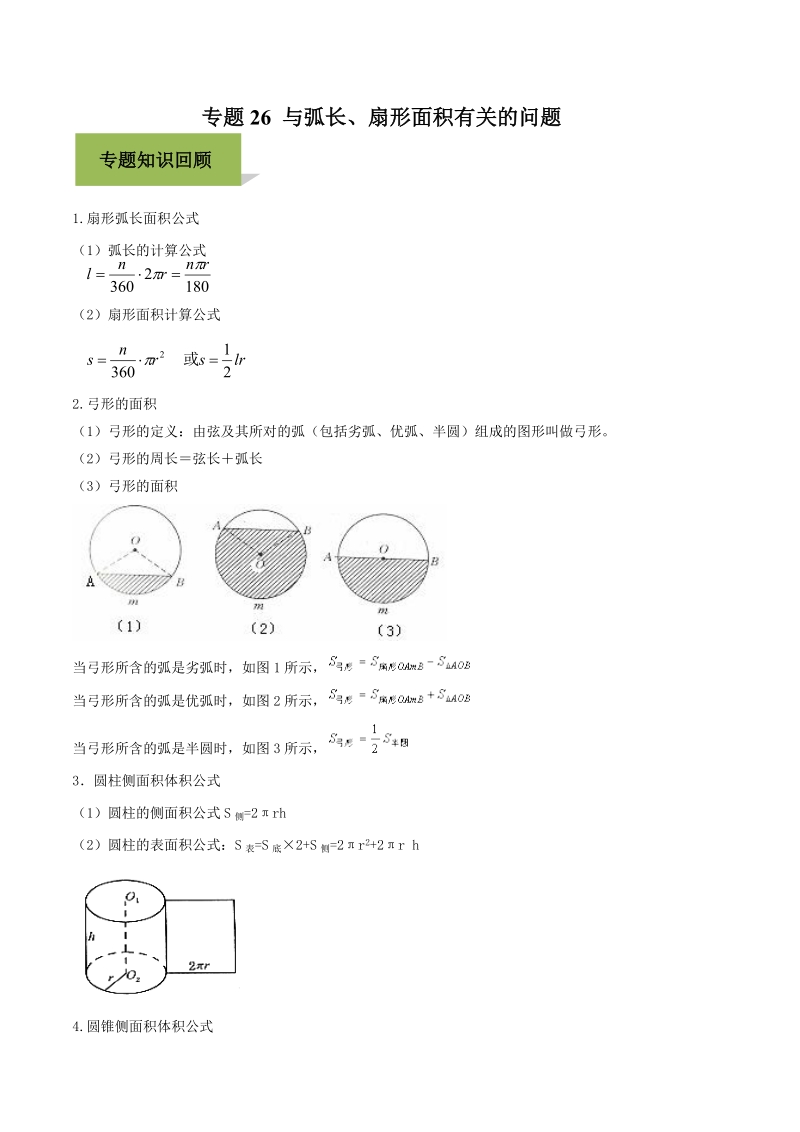



年中考数学必考专题26与弧长 扇形面积有关的问题 原创版 七七文库www 77wenku Com




扇形计算公式 百度百科



1




沪科版24 7 1 弧长与扇形面积优秀课时作业 教习网 试卷下载




09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌




弧长和扇形面积 圆ppt 第一课时 下载 牛二ppt




专题12弧长和扇形面积 原卷版 21 22学年九年级数学之专攻圆各种类型题的解法 人教版 Doc 师客文库




扇形两边长度不同如何求面积




Mathematics 数学分享站 扇形面积 Facebook




例題 扇形的面積計算練習 數學 均一教育平台




扇形的弧长及面积公式 扇形面积计算 100教育资讯网




扇形面積 Explore Facebook




04扇形面积圆2 初中数学初三 Youtube




扇形面积公式怎么算的 弧长及扇形面积的计算方法




人教版九年级上数学册 24 4弧长和扇形面积 同步练习含答案 七七文库www 77wenku Com




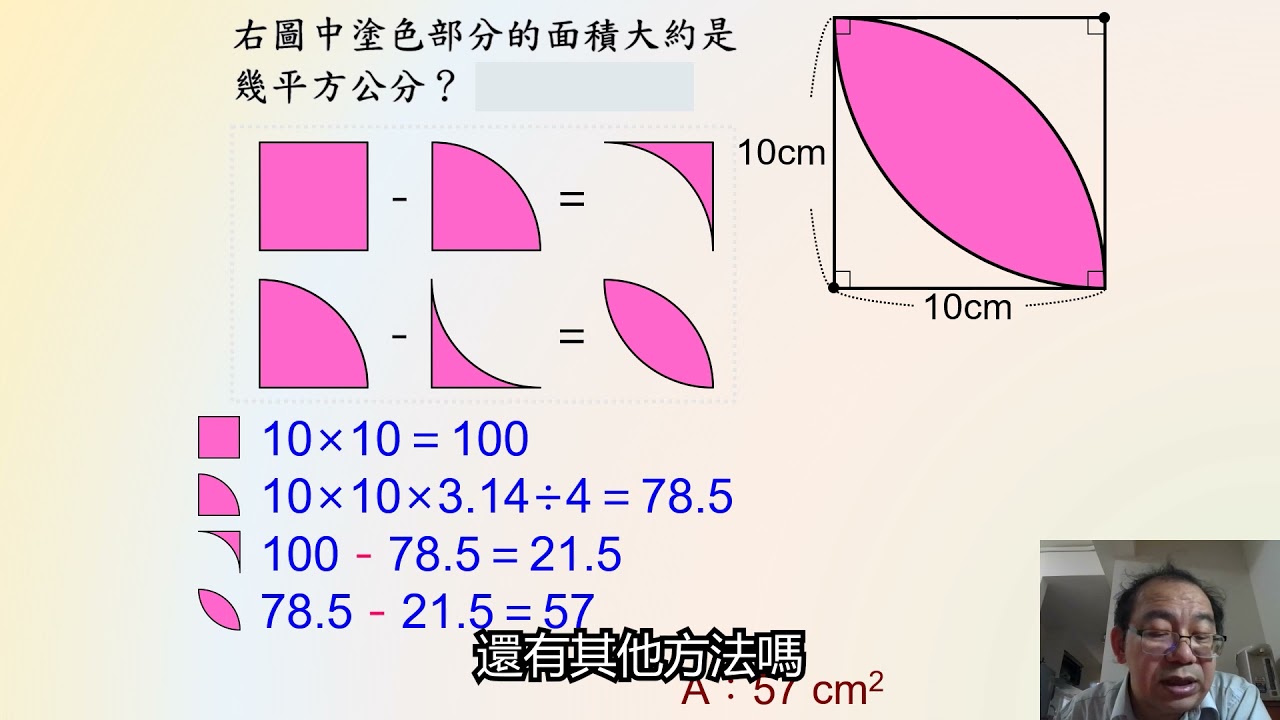
110學年度大忠四甲 數學補充 圓面積 扇形面積之葉片面積




圆扇形与弓形




弧长和扇形面积




扇形面积怎么求 小学扇形面积公式大全视频 大城生活网




人教版九年级上数学 24 4弧长和扇形面积 练习题 含答案 七七文库www 77wenku Com
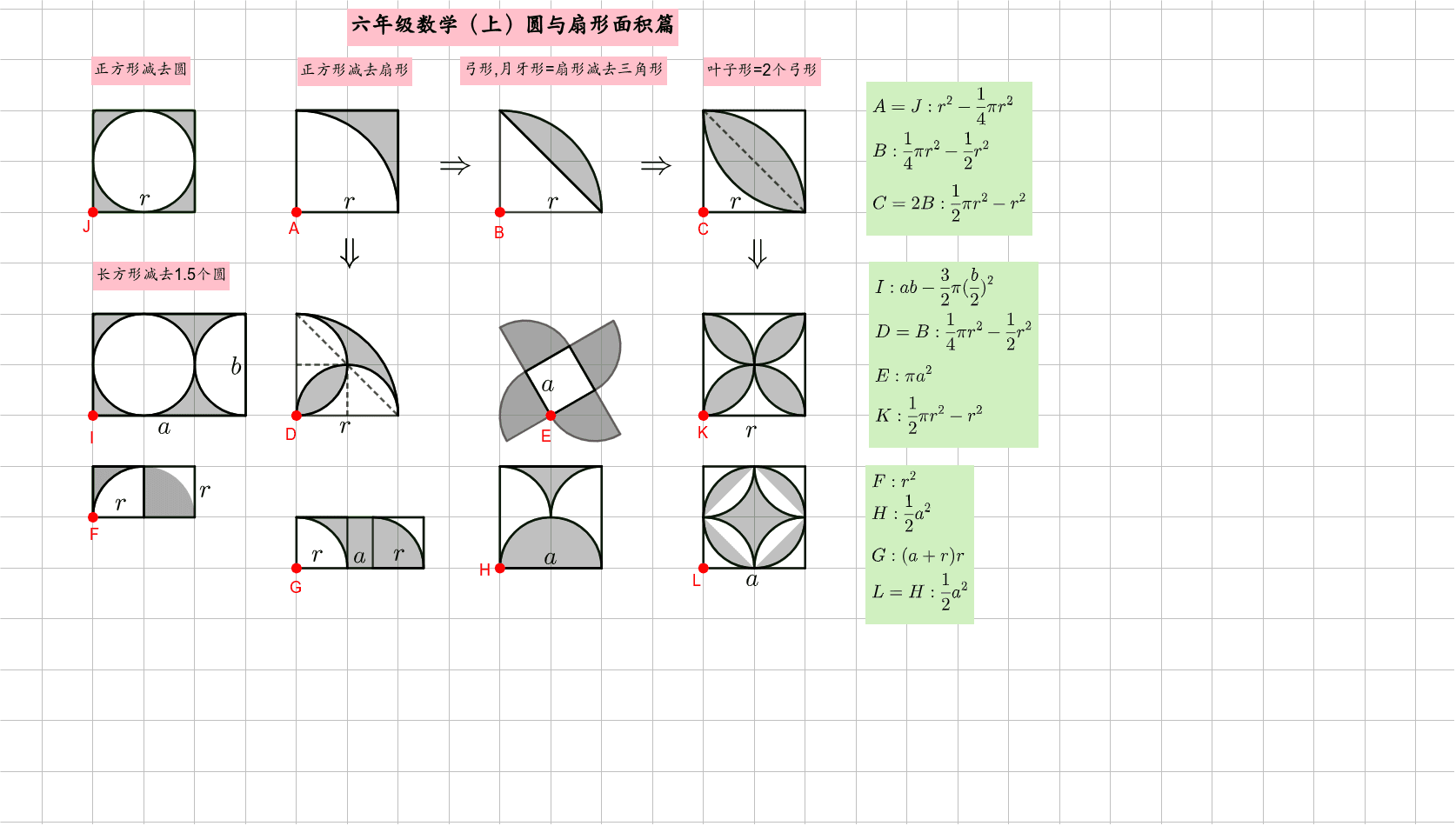



圆与扇形面积类型 Geogebra



0 件のコメント:
コメントを投稿